Earlier this year, Emma Howson posted a nice explanation of how Perl sorts a list. In short, Perl used to use quicksort and now uses mergesort. She then shows how each of those works.
I’ve never bothered to explain those in the Learning Perl class. I don’t even mention that there are different sort types or that the sort module lets you control which one you want to use. But, as someone on the path to mastery, you need to think deeply about things that you normally take for granted (and Perl lets us do some much of that).
Emma went through the algorithms that you’d learn in a computer science class, but I was curious how Perl actually does it. With a Turing machine and no sales manager breathing down your neck, everything is possible.
First, I wrote a small program to print the progress of Perl’s sort to see how it chose elements to put into $a and $b. Most of the code comes from the examples in the sort module documentation:
use v5.10;
use List::Util qw(shuffle);
{
use sort qw(defaults _quicksort);
no sort qw(stable);
my $current;
BEGIN { $current = sort::current }
say 'Using ' . $current;
my @array = shuffle( 0 .. 9 );
say "\@array is @array";
my @result = sort {
state $iteration = 1;
say "\t\$a -> $a\t\$b -> $b";
$a <=> $b
} @array;
say "\@result -> @result";
}
The output shows each comparison:
Using quicksort @array is 0 1 6 2 4 5 7 3 8 9 $a -> 2 $b -> 4 $a -> 4 $b -> 5 $a -> 6 $b -> 4 $a -> 4 $b -> 7 $a -> 4 $b -> 3 $a -> 1 $b -> 4 $a -> 0 $b -> 4 $a -> 4 $b -> 8 $a -> 4 $b -> 9 $a -> 1 $b -> 0 $a -> 3 $b -> 1 $a -> 2 $b -> 3 $a -> 2 $b -> 1 $a -> 7 $b -> 5 $a -> 6 $b -> 7 $a -> 6 $b -> 5 $a -> 8 $b -> 7 $a -> 9 $b -> 8 @result -> 0 1 2 3 4 5 6 7 8 9
But I want to know what’s happening there. The quicksort chooses a pivot then moves lower items to one side and higher items to the other. Once it does that, it takes either side and repeats the process. Eventually there’s nothing to move around.
That can be quite a bit of swapping elements, something that’s slow in the real world. The algorithm in pp_sort.c by Tom Horsley is well documented but a bit hairy.
Once I do a compare, I squeeze every ounce of juice out of it. I never do compare calls I don’t have to do, and I certainly never do redundant calls.
I also never swap any elements unless I can prove there is a good reason. Many sort algorithms will swap a known value with an uncompared value just to get things in the right place (or avoid complexity :-), but that uncompared value, once it gets compared, may then have to be swapped again. A lot of the complexity of this code is due to the fact that it never swaps anything except compared values, and it only swaps them when the compare shows they are out of position.
Perl’s quicksort starts in the middle of the list and compares that element to the element on either side to put those three elements in order. In my output, the middle element is 4 and has 2 on the left and 5 on the right. It compares those three elements:
$a -> 2 $b -> 4 $a -> 4 $b -> 5
After that, the list is the same because those three elements are already in order so it doesn’t have to swap anything. The middle number in this subset is now the pivot. That is, 4 is now the pivot.
Once those three are in order, the algorithm does work to move items less than the pivot to the left and items that are greater to the right. There’s quite a bit of arithmetic to keep track of the location of the pivot since it’s index can change. In the next part of the output, you see 4 in every comparison.
$a -> 6 $b -> 4 $a -> 4 $b -> 7 $a -> 4 $b -> 3 $a -> 1 $b -> 4 $a -> 0 $b -> 4 $a -> 4 $b -> 8 $a -> 4 $b -> 9
Notice in this section that every comparison involves 4, and when the other item comes from the right, that other item shows up in $a. When the other item comes from the left, it shows up in $b. After this series of comparisons, the internal list has been shuffled. The values of 3 and 6 swap positions in the new list:
(0 1 3 2) (4) (5 7 6 8 9)
Most of that looks already sorted because the way the input was shuffled, but elements moved to the other side were placed around the pivot. If there were elements equal to the pivot, they would move next to the pivot. There’s addition arithmetic to keep track of the size of the middle (pivot) list.
Next, the algorithm starts with 1 and does something that looks more like an insertion sort. It starts to compare the values around it:
$a -> 1 $b -> 0 $a -> 3 $b -> 1
It sees that 3 is out of position, so it checks where it should put it in relation to 1 and 2:
$a -> 2 $b -> 3 $a -> 2 $b -> 1
The left side is now sorted, although not quite a pure quicksort. I won’t go through the details here because the comments in pp_sort.c goes through some of the implementation trade-offs to avoid swapping elements until it has to. The quicksort is easy, but also a bit wasteful. For small lists, an insertion sort like we see here saves moving memory around.
(0 1 2 3) (4) (5 7 6 8 9)
When that part is done, there are two lists on either side of the pivot where the algorithm can now work again doing much of the same thing (although it’s a different section of code).
The other side is similar, comparing around 7 and finding 6 out of order, then checking where 6 should go:
$a -> 7 $b -> 5 $a -> 6 $b -> 7 $a -> 6 $b -> 5
(0 1 2 3) (4) (5 6 7 8 9)
Finally, it checks around 8 and finds all the things in order already:
$a -> 8 $b -> 7 $a -> 9 $b -> 8
Now the list is sorted:
0 1 2 3 4 5 6 7 8 9
I wanted to play with this more, so I re-implemented parts of pp_sort.c directly in Perl so I could watch it in action. I had thought about modifying the original source to insert progress statements, but I’d have to recompile perl. And, isn’t Perl’s raison d’être the quick write then run cycle? Furthermore, one of the best ways to learn a bit of code is to rewrite and debug it.
I won’t post the long code here, but you can read my Perl’s quicksort implemented in Perl gist. It’s close to the original C, although I had to use some Perly tricks since the C code uses macros.
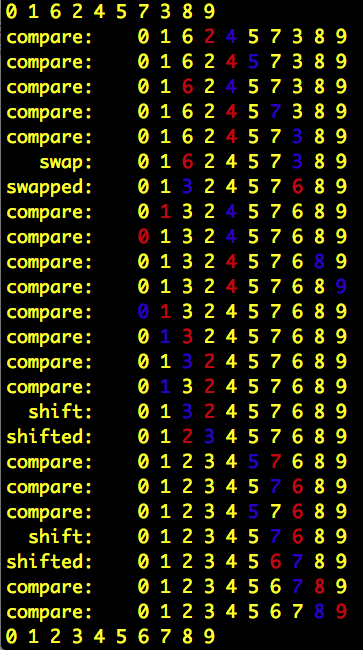
Here’s a run:
0 1 6 2 4 5 7 3 8 9 compare: 0 1 6 2 4 5 7 3 8 9 compare: 0 1 6 2 4 5 7 3 8 9 compare: 0 1 6 2 4 5 7 3 8 9 compare: 0 1 6 2 4 5 7 3 8 9 compare: 0 1 6 2 4 5 7 3 8 9 swap: 0 1 6 2 4 5 7 3 8 9 swapped: 0 1 3 2 4 5 7 6 8 9 compare: 0 1 3 2 4 5 7 6 8 9 compare: 0 1 3 2 4 5 7 6 8 9 compare: 0 1 3 2 4 5 7 6 8 9 compare: 0 1 3 2 4 5 7 6 8 9 compare: 0 1 3 2 4 5 7 6 8 9 compare: 0 1 3 2 4 5 7 6 8 9 compare: 0 1 3 2 4 5 7 6 8 9 compare: 0 1 3 2 4 5 7 6 8 9 shift: 0 1 3 2 4 5 7 6 8 9 shifted: 0 1 2 3 4 5 7 6 8 9 compare: 0 1 2 3 4 5 7 6 8 9 compare: 0 1 2 3 4 5 7 6 8 9 compare: 0 1 2 3 4 5 7 6 8 9 shift: 0 1 2 3 4 5 7 6 8 9 shifted: 0 1 2 3 4 5 6 7 8 9 compare: 0 1 2 3 4 5 6 7 8 9 compare: 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9
The output is more impressive in the terminal. I used Term::ANSIColor to highlight the elements as they go through the algorithm.
What would this look like with a pure quicksort implementation? Emma’s example is the classic algorithm:
(4) (2,9,6,5,1,8,7,3) (4,2) (9,6,5,1,8,7,3) (4,2) (6,5,1,8,7,3) (9) (4,2,1,3) (5) (9,6,8,7) (4,2,1,3) (5) (9,6,8,7) (1) (4,2,3) (5) (9,6,8,7) (1) (4,2,3) (5) (6,7) (8) (9) (1) (4,2,3) (5) (6,7) (8) (9) (1) (2) (3,4) (5) (6) (7) (8) (9) (1) (2) (3) (4) (5) (6) (7) (8) (9) (1,2,3,4,5,6,7,8,9)
Perl’s actual, non-pure implementation does something much different. First, it arranges the middle three elements before it looks for elements to swap. It’s easy to rotate elements around three consecutive elements, so it’s a quick win. When people get into the nitty gritty of implementations, they pay attention to the choice of pivot. This is also where quicksort can go horribly wrong. Choose the wrong pivot with the wrong list (say, one with many equal elements) and the algorithm goes quadratic.
Instead of shifting several elements, like you’d have to do in line 3 to move 9 to the end and move everything else down an index (and, using a temporary variable!), perl looks for two elements that can swap sides for only three copies:

Before I write my own Perl quicksort, I look for ones that already exist. Good programmers borrow; great programmers steal. I find one from Eric Storm on Stackoverflow. I don’t think he’d write it like this on his own, but he’s using the program the original questioner offered. I modified it to show the progress. Notice that there are no temporary variables since Perl handles that for you in the array slice swaps:
use strict;
use warnings;
sub qsort (\@) {_qsort($_[0], 0, $#{$_[0]})}
sub _qsort {
my ($array, $low, $high) = @_;
my @display_array = @$array;
splice @display_array, $high + 1, 0, ')';
splice @display_array, $low, 0, '(';
print "Sorting [@display_array] low: $low high: $high\n";
if ($low < $high) {
my $mid = partition($array, $low, $high);
print "\tpartition on [$mid]\n";
_qsort($array, $low, $mid - 1);
_qsort($array, $mid + 1, $high );
}
}
sub partition {
my ($array, $low, $high) = @_;
my $x = $$array[$high];
my $i = $low - 1;
for my $j ($low .. $high - 1) {
if ($$array[$j] <= $x) {
$i++;
print "\tinner swap $array->[$i] and $array->[$j]\n";
@$array[$i, $j] = @$array[$j, $i];
}
}
$i++;
print "\touter swap $array->[$i] and $array->[$high]\n";
@$array[$i, $high] = @$array[$high, $i];
return $i;
}
my @array = qw(4 2 9 6 5 1 8 7 3);
qsort @array;
print "@array\n"; # 1 2 3 4 5 7 8 9
In this example, there’s a lot of wasted copying swapping the same element with itself, which Perl is happy to do:
Sorting [( 4 2 9 6 5 1 8 7 3 )] low: 0 high: 8 inner swap 4 and 2 inner swap 4 and 1 outer swap 9 and 3 partition on [2] Sorting [( 2 1 ) 3 6 5 4 8 7 9] low: 0 high: 1 outer swap 2 and 1 partition on [0] Sorting [( ) 1 2 3 6 5 4 8 7 9] low: 0 high: -1 Sorting [1 ( 2 ) 3 6 5 4 8 7 9] low: 1 high: 1 Sorting [1 2 3 ( 6 5 4 8 7 9 )] low: 3 high: 8 inner swap 6 and 6 inner swap 5 and 5 inner swap 4 and 4 inner swap 8 and 8 inner swap 7 and 7 outer swap 9 and 9 partition on [8] Sorting [1 2 3 ( 6 5 4 8 7 ) 9] low: 3 high: 7 inner swap 6 and 6 inner swap 5 and 5 inner swap 4 and 4 outer swap 8 and 7 partition on [6] Sorting [1 2 3 ( 6 5 4 ) 7 8 9] low: 3 high: 5 outer swap 6 and 4 partition on [3] Sorting [1 2 3 ( ) 4 5 6 7 8 9] low: 3 high: 2 Sorting [1 2 3 4 ( 5 6 ) 7 8 9] low: 4 high: 5 inner swap 5 and 5 outer swap 6 and 6 partition on [5] Sorting [1 2 3 4 ( 5 ) 6 7 8 9] low: 4 high: 4 Sorting [1 2 3 4 5 6 ( ) 7 8 9] low: 6 high: 5 Sorting [1 2 3 4 5 6 7 ( 8 ) 9] low: 7 high: 7 Sorting [1 2 3 4 5 6 7 8 9 ( )] low: 9 high: 8 1 2 3 4 5 6 7 8 9
Here’s an implementation from the Algorithm Implementation wikibooks. This version ignores the memory as a physically limited resource. It uses multiple branches of recursion to descend into the list:
sub qsort {
return () unless @_;
(
qsort( grep { $_ < $_[0] } @_[1..$#_] ),
$_[0],
qsort( grep { $_ >= $_[0] } @_[1..$#_] )
);
}
qsort qw(4 2 9 6 5 1 8 7 3);
As an aside, collections of algorithms in these sorts of language comparisons are hardly ever useful. Most of them are really poor performers but the uninitiated think that shorter is better. No one really cares about these toy versions. You wouldn’t want to use that code in anything that matters. Still, that’s the Perl example. It’s also the example for many other languages, so what’s the point?
If you want to make a better quicksort, you can read Mastering Algorithms with Perl (I read it in Safari Books Online). The “Sorting” chapters goes into quicksort in great details, including an iterative solution (which is much like what perl actually does). You can learn much more about how real world constraints make the actual implementation pretty hairy (or hoary!).